The development of an idea:  from the design to the instrument.  The design of the ‘Spinetta di forma ovale’ by Bartolomeo Cristofori, Florence, 1690, Bardini Collection, Galleria dell’Accademia delle Belle Arte, Florence

Grant O'Brien

This article was first published as:   ‘Il percorso di un’idea: dal progetto allo strumento/The development of an idea: from the design to the instrument’, Bartolomeo Cristofori.  La spinetta del 1690/The 1690 oval spinet, edited by Gabriele Rossi-Rognoni, (Sillabe for the Galleria dell’Accademia, Florence, 2002) 62-81.

Introduction:

            Bartolomeo Cristofori is one of the most inventive and ingenious makers in the history of early stringed keyboard instrument making.  One of Cristofori’s most outstanding inventions is clearly the ‘gravicembalo col piano e forte’ or what we today would call the piano.  But even without having accomplished this major achievement, Cristofori would still be judged one of the finest craftsmen and designers in the field of early keyboard making and re-working.  Among the many fine examples of his work are the two ‘spinette di forma ovale’ conserved in the Galleria dell’Accademia delle Belle Arte (see the information of the Leipzig Musikinstrumentenmuseum's website[1]).  A photo of this instrument is shown below:

Oval virginal by Bartolomeo Cristofori, Florence, 1693

Musikinstrumentenmuseum of the University of Leipzig, Inv. No. 53

            Figure 1 below shows two X-rays illustrating the plan view layout of the two instruments, the 1690 Florence instrument at the top and the 1693 Leipzig instrument at the bottom[2].  The Florence instrument is unstrung, but the strings can be seen clearly on the Leipzig instrument.  The Florence ‘spinetta’ has a compass of C/E to c³ with a broken short octave in the bass with 47 notes, and the Leipzig instrument has a compass of C to c³ chromatic with 49 notes.  The Leipzig instrument with a larger number of notes is slightly wider but both instruments, having the same lowest note, have the same overall length.

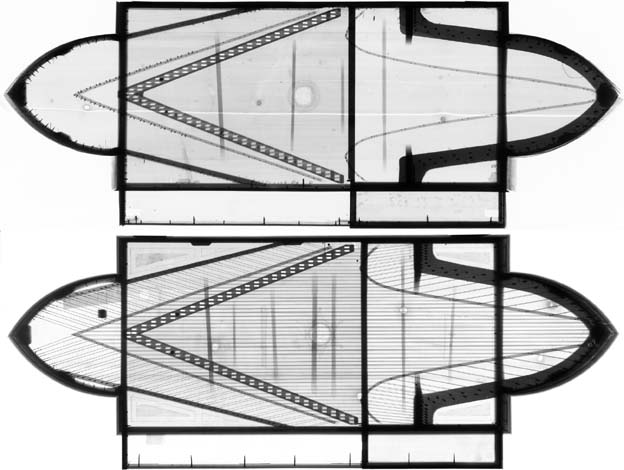
Figure 1 - Plan view X-rays of the ‘spinette ovali’ of 1690, Florence (above) and of 1693, Leipzig (below) both by Bartolomeo Cristofori.

            There are, however some other obvious differences between the two instruments.  The diagonally-placed hitchpin rails extend beyond the corners of the rectangular central part of the case in the Leipzig instrument and reach past these corners to intersect the curved ends of the instrument on the left-hand side.  In the Florence instrument these hitch-rails stop at the corner of the rectangular central part of the case and the curved end portions.  The bass end of the bridges in the Florentine instrument are back-pinned and the angles of the hitchpin ends of the strings are gradually reduced until they become parallel with the sounding portion of the strings for the lowest notes.  The right-hand ends of the bass sections of the bridges are mitred in the Leipzig instrument, thus pushing the ends of the bridges at the right-hand end further apart and closer to the case sides in the bass.  In addition there are clearly fewer soundbars below the soundboard of the Florence instrument, although it is likely that some of the soundbars in the much-restored Leipzig instrument are not original.

            Technically these instruments are actually a type of virginal.  Although other definitions are admitted, the preferred organological definitions of the harpsichord, spinet and virginal are set out clearly in the recent editions of The New Grove Dictionary of Music and Musicians[3].  According to these definitions a virginal is a term “which applies to instruments whose strings run at right angles to the keys, rather than parallel with them as in a harpsichord or at an oblique angle as in a spinet”.  In the Florence and Leipzig instruments the keys and strings are exactly at right angles to one another.  But unlike a normal virginal with the treble strings placed at the back of the instrument and the bass strings along the front, here the shortest strings are placed alternately near the outside edges of the instrument and the longest strings are placed centrally.  Because of this, alternate keys operate jacks which pluck strings on opposite sides of the case.  Therefore although this instrument has traditionally been called a ‘spinetta’ it is technically a virginal and cannot therefore be designated as a spinet at least in English[4].  I have, however, chosen here to use the Italian form and to call it a ‘spinetta’ or ‘spinetta ovale’.  Like the Flemish muselar virginals and most (but not all) Italian virginals both the left- and right-hand bridges are free to vibrate and therefore there is no nut in the usual sense.

The use of the unit of measurement in the design of instruments:

            The city or region of construction of an anonymous instrument can be determined by analysing the size of the unit of measurement used in its construction.  Until the time of the Napoleonic invasions of the Italian peninsula each of the major centres in Italy used its own unit of measurement, and the size of these units varied from place to place.  The canna, braccio, piede, palmo, etc. and their subdivision into the oncia, soldo or pollice therefore characterized  each of the centres in which instruments and virtually all other manufactured items were built.  Therefore if the unit of measurement used in the design and construction of an anonymous instrument can be determined, this can be used in turn to establish the centre of its origin.  Once established, the unit of measurement can then be used to analyse the string-scaling design, the layout of the keys and jacks, and all of the other design elements of an instrument.

            It is quite clear that any maker of instruments - or any other object for that matter - would have worked on a day-to-day basis using convenient numbers and uncomplicated fractions of his local unit of measurement.  For the obvious reason that whole numbers or simple fractions are easy to remember an artisan would work in convenient units of measurement when he is designing and executing the object he is making.  Because most of the measurements used can be made, to a certain extent at least, arbitrary there is no need to invoke complicated numbers in their design.  Most of the measurements used by hand-workers, artisans, artists, architects, designers and all of those involved in industry and commerce were based on simple numbers of the basic unit of measurement, or on their simple subdivision.

            Only where it is really necessary and where dictated by some rule or theoretical concept would an instrument builder use a complicated or irrational division of the local unit of measurement in his design.  This has been shown clearly from the ground-breaking study of musical instruments of many types made by Herbert Heyde[5].  Further work that I have done recently in this field shows that the maker began his design by drawing out the baseboard using dimensions which were simple integers or fractions of the local unit of measurement.  The case sides that he then applied to the outer edges of the baseboard were cut to a height also equal to a simple number (or number plus simple fractions) of the local measurement unit.  Similarly the position and measurements of all of the other design features of the instrument were made by choosing simple numbers of the local unit of measurement.  Clearly which measurements were chosen by a maker in simple numbers would depend on his method of working and especially on the order in which the various operations necessary to construct the instrument were carried out.

            Normally the unit of measurement can be determined for a harpsichord or a polygonal virginal because the makers used a simple geometrical construction to arrive at the tail angle of their harpsichords or the end angles of their virginals[6].  However because of the unusual nature of the geometry of the case outline of this instrument no analogous procedure can be used.  Instead, given that the maker and where he worked are already known, the unit of measurement used by Cristofori is also known and can be applied to the various dimensions of the baseboard and case, to the jack and string spacing layout, to the keyboard, and to the string-scaling design.  In fact the Florentine unit of measurement was used for all aspects of the design of this instrument even though only those just mentioned will be dealt with here.

The Florentine braccio, palmo and soldo

            During the historical period before the Napoleonic invasion a number of units of measurement was used in Florence.  These included long units like the cavezzo and the canna agrimensoria with lengths of about 3.3 metres and 2.7 metres, as well as a number of mercantile units for measuring different types of cloth.  However the most common units of measurement used for measuring most day-to-day items such as land, buildings, furniture, etc. were the braccio, the palmo and the soldo.  The braccio was divided into two palmi each of 10 soldi, so that the braccio had a length of 20 soldi.  There were also further rather complicated subdivisions of these units[7]. 

            There has been, and there still is, some confusion about the sizes of the Florentine units of measurement during the historical period.  The problem has arisen because the length of the unit of measurement in Florence was re-defined by legislation passed on 2 July, 1782.  According to this legislation the unit of length was increased by a factor of 17/16 (an increase of 6¼%).  However, most of the references giving the Florentine units were published in the nineteenth century during the period after the adoption of the metric system, and these references therefore give the length of the longer post-legislation unit rather than the shorter unit that was used during the period of early keyboard instrument making in Florence.  Angelo Martini, in his Manuale di metrologia[8], is one of the few late nineteenth-century authors to give the length of the braccio and soldo before the standard of length in Florence was re-defined by law[9].  Martini gives the length of the braccio as 551.202mm which gives a palmo of half this or 275.60mm and a soldo of 27.56mm.  It is this value of the braccio and soldo that have been used here.

            However, as mentioned above, the lengths of the Florentine units were increased after 1782, and most sources give the braccio a length of about 583.6mm so that the soldo would have a length of 29.18mm.  As might have been expected this unit did not work when applied to the various dimensions of this instrument.  And this larger unit does not work in the analysis of other instruments by Cristofori, nor in instruments by the Florentine makers Francesco Poggi and Stefano Bolcioni which I have analysed[10].

The case design of the ‘spinetta ovale’:

            In the analysis of the design and layout of the baseboard and case I have taken my measurements from an electronic copy of the drawing made by Tony Chinnery[11] and not from the instrument itself.  The analysis of the unit of measurement and the geometry of the instrument begins most easily with an analysis of the two rounded ends of the ‘spinetta ovale’.  The drawing of these ends was made by Tony Chinnery by drawing their shapes using a best fit sub-routine of the drawing programme called a spline.  It was noticed immediately that each of these spline curves could be accurately represented by a single arc of constant curvature.  Each spline curve was therefore substituted for a single arc drawn using the beginning end, mid-point and finishing end of the spline curve as the three defining points of the arc.  The radius of the arcs drawn in this way were found to be 382.61mm, 379.66mm, 393.54mm and 387.45mm.  The average radius of these arcs is 385.8mm.  Using Angelo Martini’s value of the Florentine soldo (see Footnote 8) this gives a radius expressed in soldi of 13.999, clearly intended by Cristofori to be exactly 14 soldi.  The distances between the ends of the arcs intersecting the rectangular central section of the instrument are 358.9mm at the left-hand end and 361.8mm at the right-hand end.  The average of these two is 360.35mm or 13.08 soldi.  Hence this distance must have been intended to be exactly 13 soldi so that the centres of the arcs making up the curved ends must have been displaced 1 soldo from the internal ends of each of the arcs.  The geometry of the construction of the shape of the ends of the case can be seen below in Figure 2.

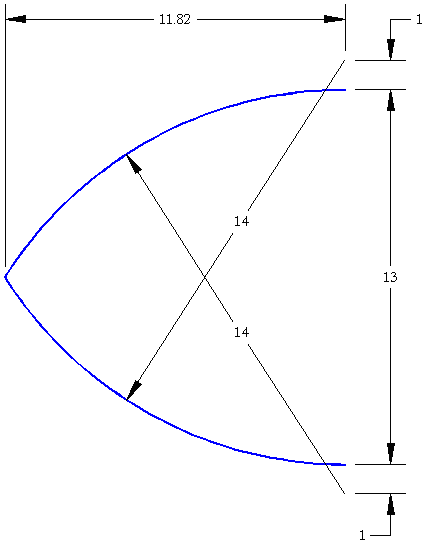
Figure 2 - The geometry of the curved ends of the case measured in Florentine soldi.

            Because of the curved shape of the ends and because of the particular geometry used by Cristofori in constructing the ends of the instrument the total projection of the ends does not result in a rational number when expressed in soldi.  Instead this projection is close to 325.8mm or 11.82 soldi (see Figure 2.

            Measured from the drawing, the total length of the baseboard between the extreme points of the rounded ends is measured to be 1821.4mm = 66.08 soldi or very close to 66 soldi.  Because the projection of the two ends of the case is an irrational number when expressed in soldi the lengths of the rectangular sides of the baseboard of the instrument will therefore also result in irrational numbers when expressed in soldi.  Without going in to the details of all of the measurements of the different elements of the baseboard layout, it can be shown that the measurements used by Cristofori to design the baseboard layout are given in Figure 3 shown below where the measurements indicated are all given in Florentine soldi. 

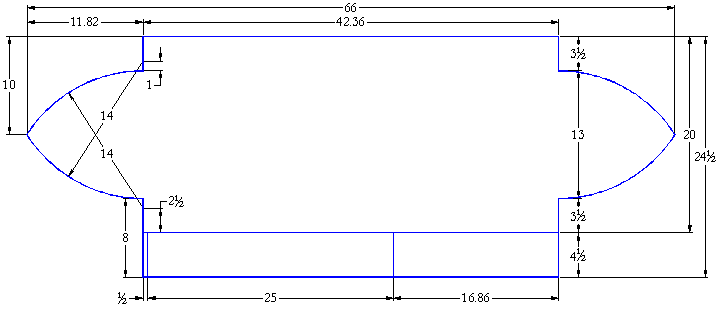
Figure 3 - The design of the baseboard layout

            Here it can be seen that most of the measurements are simple numbers of Florentine soldi but that a number of resultant measurements are irrational numbers resulting from the geometry of the curved ends of the case.  The one particularly noteworthy measurement among these is the internal width of the case without the projection for the keyboard and toolbox.  This is 20 soldi or exactly one braccio, the fundamental unit of the Florentine measuring system.

            The case height has been measured to be 172mm or 6.24 soldi, clearly intended to be 6¼ soldi[12].  Similarly the height of the soundboard liners, and the dimensions of the rose, the liners and all of the other parts of the instrument case originally measured out by Cristofori can be shown to be close to a simple number of Florentine soldi.

The keyboard and jack layout design:

            The average 3-octave span of the keyboards measured from the drawing is 495.7mm.  Converted to Florentine soldi this gives 17.99 soldi and this must have been intended by Cristofori to be exactly 18 soldi[13].  Therefore one octave of keys was designed to be 6 soldi wide[14].  Also measured from the drawing the sideways displacement in a direction parallel to the length of the instrument from the right-hand edge of the front C/E jackslot to the corresponding edge of the top c³ jackslot is 633.5mm.  Within this sideways spacing there are 46 pairs of jackslots so that the average spacing is .  Clearly, the rows of jackslots were intended by Cristofori to be separated by exactly ½ soldo, so that the spacing between successive alternate jackslots would be just one soldo.  Because the spacing of successive jackslots is ½ soldo, this would also be the width marked out for the tails of the keylevers.  The width of twelve notes in an octave would therefore be 6 soldi, the same as that just found for the octave spacing of the fronts of the keylevers.  Hence, at least for the part of the compass outwith the bass broken octave[15], there is no need for key cranking in this instrument:  the width of one octave of keyfronts is the same as one octave of keytails as indeed is usual (but not universal) for most stringed keyboard instruments other than the clavichord.

            In order to analyse the lateral spacing of the strings and jackslots, the positions of the long 8' bridge pins were measured relative to the inside of the front of the instrument.  Because of the delicacy of the instrument only the measurements for the strings along the straight section of the case nearest the player were measured.  Hence the data cover only the bridge pins for the notes from c to c³.  These measurements are given in Table 1 below.

                                                     Note                    Note              Distance to

                                                  number                 name              nameboard

                                                       47                         c³                         31

                                                       45                        b^b2                        42

                                                       43                        g^#2                        52

                                                       41                         f^#2                         63

                                                       39                         e²                         73

                                                       37                         d²                       84½

                                                       35                         c²                        94½

                                                       33                        b^b1                       105

                                                       31                        g^#1                       116

                                                       29                         f^#1                        126

                                                       27                         e¹                        137

                                                       25                         d¹                        148

                                                       23                         c¹                        159

                                                       21                         b^b                      169½

                                                       19                         g^#                        180

                                                       17                         f^#                        191

                                                       15                          e                         203

                                                       13                         d                         213

                                                       11                          c                       223½

Table 1 - Position of the long 8' bridge pins from the back of the nameboard in mm.

          These distances are plotted in the graph shown below in Figure 4.

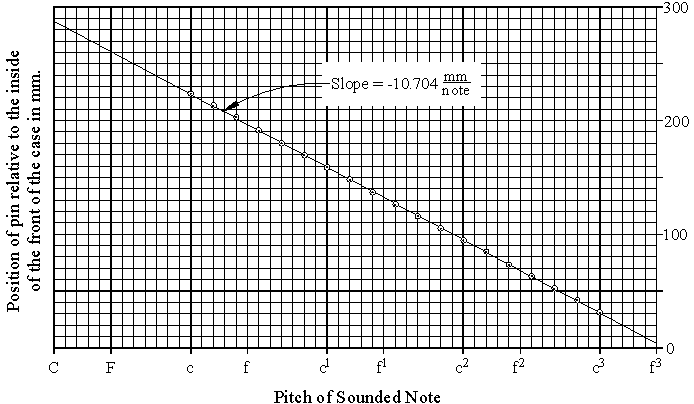
Figure 4 - Lateral string spacing of the bridge pins of the long 8' strings.

            The points on the graph were fitted to a straight line using the usual regression analysis method of least squares[16].  The regression analysis shows that the relative spacing of the successive bridge pins for the long 8' strings is 10.704 with an excellent correlation coefficient of 0.999964, and a standard error of 0.022 (percentage error of only 0.2%).  With this relative spacing the total width of all of the strings ranging over a compass of C/E to c³ with 45 notes would be mm.  Expressed in Florentine soldi, this amounts to 481.7mm/27.56 = 17.48 soldi.  Quite clearly this must have been intended by Cristofori to be exactly 17½ soldi[17] (error only 0.1%). 

          This result has a number of important and interesting implications.  First of all this instrument actually has 47 notes (the 45 notes of the C/E to c³ compass plus the two additional split accidental notes D/F^# and E/G^# of the broken octave) and not 45.  Apparently Cristofori therefore seems to have envisaged the design initially as a simple C/E to c³ short-octave instrument with 45 notes.  The lateral width of 45 pairs of jackslots in this design had then later to be increased by the width of two pairs of jackslots when the D/F^# and E/G^# notes were added.

          Also the space he devoted to the successive pairs of strings in this instrument is considerably less than that which he used in his harpsichords.  Unpublished research by me[18] has shown that normally Cristofori spaced out the pairs of strings in his harpsichords using a distance close to or exactly equal to ½ soldo = ½x27.56mm = 13.78mm (related to the octave span of the keyboard as shown above) and not the much smaller spacing of 10.704mm which he used here.  So far as the relative spacing of the strings is concerned, however, the amount of space required for the strings and jacks is the same in this instrument as that required in a spinettone[19] with two sets of strings (either 2x8' or 1x8',1x4') and with the jacks all in a straight line.

            The above analysis shows that the sideways displacement of each pair of jacks was just half a soldo and that the spacing front-to-back of each pair of jackslots was 17½ soldi/45 jackslots = 17½ x 27.56mm/45 jackslots = 10.718mm/jackslot which is close (difference = 0.1%) to the value determined above in the graph of Figure 4.

            The design of the spacing of the jackslots expressed in Florentine soldi is shown in the diagram in Figure 5 below:

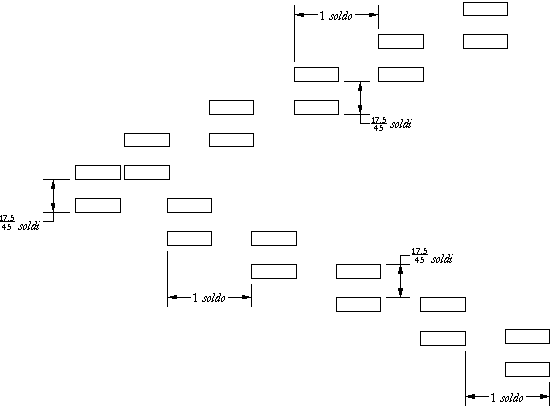
Figure 5 - Jackslot layout design

            The 47 pairs of jackslots are grouped centrally between the front and back case sides so that the long bass C strings are placed almost in the centre of the instrument.  There are then 23 pairs of strings on either side of the central C/E strings making up the 47 notes of the compass.  Effectively this results in the centres of the two outside jackslots (those for the short strings of both b^I2 and c³) each being placed about one soldo from the inside edges of the central part of the instrument.  The Leipzig spinetta ovale has 49 notes in its chromatic C to c² compass which is 2 more than in this instrument.  This would require an additional space of 2x17½ soldi/45 = 35/45 soldi, or almost one soldo.  The difference in the width of the central portion of the case is 589mm - 563mm[20] = 26mm = 0.94 soldi.  It therefore appears that Cristofori made the Leipzig instrument (with two more notes than the Florence instrument) by giving it a width one soldo wider by adding half a soldo to each side of the central portion of the case.

The string scaling design:

            Both the string scalings and the plucking points can be measured from the drawing made by Tony Chinnery[21].  The plucking points were measured, carefully taking into account the asymmetrical arrangement of the tongues in the jacks for the register plucking towards the player and that plucking away from the player[22].  These are given below in Table 2 where the string lengths and plucking points of the c notes have been highlighted in light grey, and of the f notes in dark grey. 

Table 2 - String lengths and plucking points in mm and soldi

            The string lengths of both the long and short strings are plotted below in Figure 6.

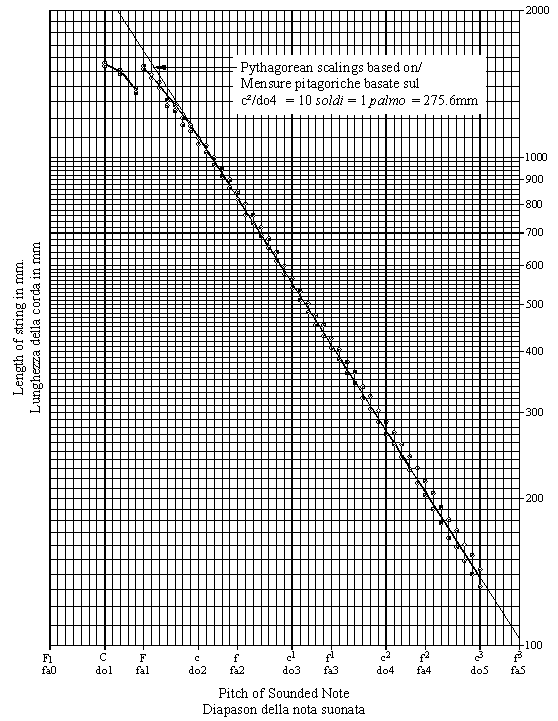
Figure 6 - The scalings of the short and long strings

            Both Table 2 and Figure 6 show that the string scaling design used by Cristofori was based on the Florentine soldo.  It is important to realise that for this instrument it was necessary to lay out lengths and plucking points for both the c and the f notes.  The bridges nearest the player were positioned relative to one another and relative to the jacks using the c notes, and the bridges furthest from the player using the f notes.  Indeed the f (and the b) notes are marked near the furthest right-hand bridge as an aid to the builder to help him keep track of the positions of the strings for these notes.  The average length of the c notes is clearly based on the braccio, the palmo and half a palmo, with the lengths of middle c¹, c² and c³ all having values close to these measures when expressed in units of the soldo[23].  In Pythagorean theory the lengths of the treble f notes should be 1½ times each of these and so should therefore be 7½, 15, and 30 soldi, and indeed Table 2 shows this to be the case with only a small error.  The plucking points of the long strings are also very regular in their values.  Beginning at the top note and working downwards the c notes have plucking points of 2½, 3½, 4½, 5 and 5¼ soldi, and the f notes have plucking points of 3, 4, 5 and 5½ soldi.  The highlighted notes in Table 2 are all close to simple numbers when expressed in Florentine soldi, whereas the intermediate notes can be seen to give untidy numbers because they are not the result of Cristofori’s design intention, but consequent to it.

            The lengths of the long and short strings of each of the notes are plotted in the graph of Figure 6.  Superimposed on these a thin straight line has been drawn for Pythagorean string lengths which are based on c² = 10 soldi = 1 palmo = 275.6mm.  This straight line passes neatly between the measurements for the long and short strings for each note, again indicating that it is the average c and f scalings that were laid out by Cristofori when he positioned his bridges.

            It would therefore appear that the left-hand bridges were positioned by Cristofori by marking their location out using the plucking points of the long strings of each pair, and that the position of the two right-hand bridges were located after the pins had been placed in the left-hand bridges by measuring out a length from a position half-way between each of the two left-hand bridge pins.  No other reasonable suggestion to explain this suggests itself to me.

Modifications to the design:

            It is clear from the analysis above that Cristofori changed his original design from that of an instrument with a simple C/E to c³ short octave compass with 45 notes to one with a bass broken short octave with 47 notes.  Presumably the original design would have had an inside case width of 19 soldi, and this was then changed to the present width of 20 soldi or 1 braccio.  The 49-note ‘spinetta ovale’ in Leipzig, with a chromatic C to c³ compass, was further widened to 21 soldi to make room for the extra 2 notes required.

            A much less fundamental alteration to the design of the instrument involves a change to the hitchpin positions and the backpinning of the left-hand bridges.  There are various plugged holes near the hitchpins on both sides of the instrument.  The first set of plugged holes is next to the hitchpin for the note b^I1 on the near bridge and near the note b¹ on the far bridge.  There then appears to be a number of plugged holes in the rows of hitchpins all the way down to the bass.  In other words Cristofori seems to have been happy with the positioning of the treble octave of notes but re-positioned the hitchpins from that point onwards.  The positions of these plugged hitchpin holes have been added to the drawing by Tony Chinnery[24].

            Using this drawing the angle of the strings coming off the bridge pins to the hitchpins has been measured using the AutoCAD programme.    Straightforward analysis shows that the original positions of the hitchpins give a more-or-less constant side-draft angle near 15½º to 16º throughout virtually the whole of the compass.  In the altered design it is only the top octave of notes which have this angle and then the side draft gradually reduces until there is no side draft at all.

            Quite why Cristofori changed his mind and decided to reduce the angle of the bass strings and back-pin the bass bridge pins can only be surmised[25].  By the time he came to design the 1693 ‘spinetta ovale’ now in the Musikinstrumentenmuseum in Leipzig he had reverted to the original scheme and had opted for maintaining the angle of the strings throughout the compass for both sets of bridges without any backpinning.

Conclusions:

            The ‘spinetta ovale’ of 1690 by Bartolomeo Cristofori is cleanly and cleverly designed.  It is evident from the above analysis that the design of the case, the keyboard and jack layout, and the string scaling and plucking point design were carried out using the Florentine soldo, and that the length of the soldo was that in normal usage in Florence before the legislation passed in 1782 changed the standard of length in Tuscany.

            The only major alterations to Cristofori’s initial design involved increasing the compass by the two notes D/F^# and E/G^# to change the initial normal short octave to a broken octave.  He also changed the side-draft angle of the strings between the bridge pins and the hitchpins, and this seems to have been done either for aesthetic reasons or for structural reasons to avoid the large forces associated with the heavy, highly-tensioned bass strings.

- Dr Grant O’Brien

              - Edinburgh, October, 2002