![]()
The case, stringing and fretting design of the 1543 Venetian clavichord by Dominicus Pisaurensis
an article published in De Clavicordio, Proceedings of the V International Clavichord Symposium/Atti del V congresso internazionale sul clavicordo. Magnano, 5-5 September 2001, edited by Bernard Brauchli, Alberto Galazzo and Ivan Moody, (Musica antica a Magnano, Magnano, 2002), 91-107, by Grant O'Brien
Recent work that I have done on the use of the local unit of measurement to design and build historical keyboard instruments suggests that the use of simple units of the local unit of measurement was as fundamental to the design of the string scalings as it was to the design and construction of the case[1]. For example, instruments made in different centres throughout Italy and designed for yellow brass stringing and tuned to normal reference pitch R would have treble scalings based on a length for c2 given in the following table[2]:
|
Number of units |
Length of c2 |
Centre |
Unit |
Length of unit |
|
10 soldi = 1 palmo = ½ braccio |
275.6mm |
Florence |
soldo |
27.56mm |
|
7½ once |
272.0mm |
Milan |
oncia |
36.265mm |
|
13 once |
283.9mm |
Naples |
oncia |
21.835mm |
|
15 once |
279.3mm |
Rome |
oncia |
18.619mm |
|
10 once |
289.8mm |
Venice |
oncia |
28.98mm |
Table 3 - Common c2-equivalent scalings of brass-strung harpsichords and virginals
Indeed it is likely that the local variation in pitch from one centre to another in Italy and elsewhere arose because the design and construction of instruments, and especially of organs, was based on the different local units of measurement. Brass-strung harpsichords, virginals and clavichords designed using each of these local units of measurement would, however, all sound well at roughly the same pitch. This suggests that instruments using other stringing materials like iron and red brass were also designed using scalings based on a simple number of the local units of measurement.
Hence it would seem to be worthwhile to look at normal iron, yellow brass and red brass string scalings and to compare them with simple numbers of Venetian once when considering a clavichord like the one made and designed by Pisaurensis. This is done in Table 4 below.
|
|
At ‘normal’ pitch R |
At a pitch of R + 5 |
|||||||||
|
|
|
|
Venetian measurement |
Venetian Measurement |
|||||||
|
Material |
Taskin's scalings |
Ruckers' scalings |
|||||||||
| c-based scalings | g-based scalings |
c-based scalings |
|||||||||
|
once |
mm |
once |
mm |
once |
mm |
||||||
|
Iron |
364.0mm |
355.0mm |
12 |
347.8 |
8 |
231.8 |
8 |
231.8 |
|||
|
Yellow brass |
292.6mm |
289.5mm |
10 |
289.8 |
6 |
193.2 |
6 |
193.2 |
|||
|
Red brass |
231.4mm |
211.2mm |
8 |
231.8 |
5 |
154.6 |
5 |
154.6 |
|||
Table 4 – Typical French and Flemish scalings compared with some simple Venetian measurements
From Table
4
it is clear that the normal seventeenth and eighteenth-century scalings found in North-European instruments are close to
c2 scalings based on 12, 10 and 8 Venetian once for iron, yellow brass and red brass stringing respectively. For the note
g2 a fifth higher than c2, the corresponding scalings would just be ![]() those of
c2 and these are shown near the middle of Table 4 Thus for an instrument pitched a fifth higher than reference pitch at R + 5, iron, yellow brass and red brass stringing would correspond to
c2–equivalent scalings of 8, 6
those of
c2 and these are shown near the middle of Table 4 Thus for an instrument pitched a fifth higher than reference pitch at R + 5, iron, yellow brass and red brass stringing would correspond to
c2–equivalent scalings of 8, 6![]() and 5
and 5![]() Venetian once respectively (shown on the right-hand side of Table 4).
Venetian once respectively (shown on the right-hand side of Table 4).
Let us look therefore at the scalings of the Pisaurensis clavichord to see whether or not any aspect of the stringing of this instrument fits into this pattern. The string lengths for each note with the bridges in their present positions are given in Table 5 below.
|
Length |
|
Note |
Length |
|
|
c3 |
117½ |
|
c#1 |
398 |
|
b2 |
126 |
|
c1 |
418 |
|
bb2 |
132 |
|
b |
450½ |
|
a2 |
141 |
|
bb |
466½ |
|
g#2 |
150½ |
|
a |
476½ |
|
g2 |
159 |
|
g# |
510 |
|
f#2 |
168½ |
|
g |
534½ |
|
f2 |
178 |
|
f# |
545 |
|
e2 |
188½ |
|
f |
570 |
|
eb2 |
198½ |
|
e |
581 |
|
d2 |
210 |
|
eb |
601½ |
|
c#2 |
224½ |
|
d |
733 |
|
c2 |
234½ |
|
cT |
745 |
|
b1 |
246½ |
|
c |
756 |
|
bb1 |
259 |
|
B |
766 |
|
a1 |
274½ |
|
Bb |
779 |
|
g#1 |
287½ |
|
A |
869 |
|
g1 |
302 |
|
G |
894 |
|
f#1 |
321 |
|
F |
919 |
|
f1 |
335 |
|
E |
880 |
|
e1 |
347½ |
|
D |
904 |
|
eb1 |
361½ |
|
C |
933 |
|
d1 |
386 |
|
|
|
Table 5 – String scalings as measured with the bridges in their present positions
Leipzig Musikinstrumentenmuseum der Universität, Clavichorde, Cat. No. 1
These scalings are plotted in the graph shown in Figure 2 below. This graph shows the pitches of the played notes at the bottom of the graph and, assuming that the instrument was designed to sound at a pitch of R + 5, with the actual sounded pitch given at the top of the graph. In all of the discussions below unless otherwise stated the notes referred to are the played notes, not the sounded notes.
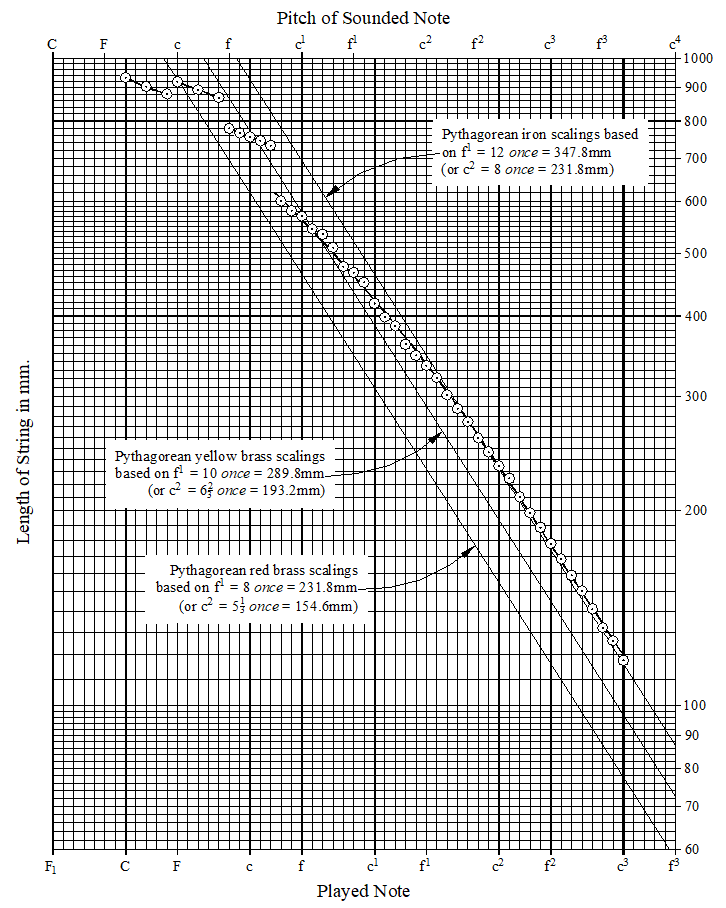
Figure 2 – Measured scalings with the bridges in their present positions
Leipzig Musikinstrumentenmuseum der Universität, Clavichorde, Cat. No. 1
The graph shown in Figure
2
is plotted on semi-logarithmic graph paper. This is used because it makes Pythagorean scalings, which double and halve with each octave drop and rise in pitch, plot as straight lines. Indeed Pythagorean scalings for
c2-equivalent scalings given by 8, 6![]() and 5
and 5![]() Venetian once have been drawn on this graph, and all of these correspond to straight lines.
Venetian once have been drawn on this graph, and all of these correspond to straight lines.
Comparing the theoretical thin lines for Pythagorean
c2 scalings of 8, 6![]() and 5
and 5![]() Venetian once with the measured scaling in the treble it is clear that the line formed by the measured points is close to the theoretical line for iron scalings (c2 =
8 once at a pitch of R + 5) but deviates gradually more and more for the notes at the extreme treble end of the compass. The measured length of
c2 itself is 234½mm, about 2.7 mm longer than 8 Venetian once = 231.84mm. The measured lengths in the extreme treble are also about 2.7mm too long when compared to the theoretical line, and this suggests that the whole treble bridge is now about 2.7 mm too far away from the tangents.
Venetian once with the measured scaling in the treble it is clear that the line formed by the measured points is close to the theoretical line for iron scalings (c2 =
8 once at a pitch of R + 5) but deviates gradually more and more for the notes at the extreme treble end of the compass. The measured length of
c2 itself is 234½mm, about 2.7 mm longer than 8 Venetian once = 231.84mm. The measured lengths in the extreme treble are also about 2.7mm too long when compared to the theoretical line, and this suggests that the whole treble bridge is now about 2.7 mm too far away from the tangents.
On the other hand the measured length of tenor c is somewhat short of the theoretical line for yellow brass stringing based on
c2 = 6![]() Venetian once. At a pitch of tenor c two octaves lower than c2
the equivalent of c2 = 6
Venetian once. At a pitch of tenor c two octaves lower than c2
the equivalent of c2 = 6![]() once is
once is ![]() once
= 26
once
= 26![]() once = 772.8mm. The measured length of tenor c is 756mm which is about 16.8mm less than this value. Therefore moving the middle bridge away from the tangents by this amount would bring it into agreement with the theoretical value for yellow brass stringing above this note. In a parallel way the third bridge would also have to be moved away from the tangents by 8.4mm at the note F in order to position it at a distance of 4x8
once
= 32 once = 927.36mm. Instead of giving an F scaling of 919mm as it does in its present position it would then be in a position where it would correspond to a red brass
f2-equivalent scaling of exactly 8 once (ie a c2 scaling of
5
once = 772.8mm. The measured length of tenor c is 756mm which is about 16.8mm less than this value. Therefore moving the middle bridge away from the tangents by this amount would bring it into agreement with the theoretical value for yellow brass stringing above this note. In a parallel way the third bridge would also have to be moved away from the tangents by 8.4mm at the note F in order to position it at a distance of 4x8
once
= 32 once = 927.36mm. Instead of giving an F scaling of 919mm as it does in its present position it would then be in a position where it would correspond to a red brass
f2-equivalent scaling of exactly 8 once (ie a c2 scaling of
5![]() once transposed).[3]
once transposed).[3]
The lengths
c2 = 8 once, c = 26![]() once, and F = 32 once could be considered to be the critical design scalings for this clavichord corresponding to notes critically stressed just at their breaking points for the materials iron, yellow brass and red brass respectively. It is also, in my view, these lengths that determine the correct positions of each of the three moveable bridges. This has been shown diagramatically below in Figure
3
where a plan view of the instrument is shown along with the fret positions and the string pairs for each of the critical design notes. The green lines show the new positions of the bridges which would have to be moved from their old positions in order to achieve these critical design scalings.
once, and F = 32 once could be considered to be the critical design scalings for this clavichord corresponding to notes critically stressed just at their breaking points for the materials iron, yellow brass and red brass respectively. It is also, in my view, these lengths that determine the correct positions of each of the three moveable bridges. This has been shown diagramatically below in Figure
3
where a plan view of the instrument is shown along with the fret positions and the string pairs for each of the critical design notes. The green lines show the new positions of the bridges which would have to be moved from their old positions in order to achieve these critical design scalings.
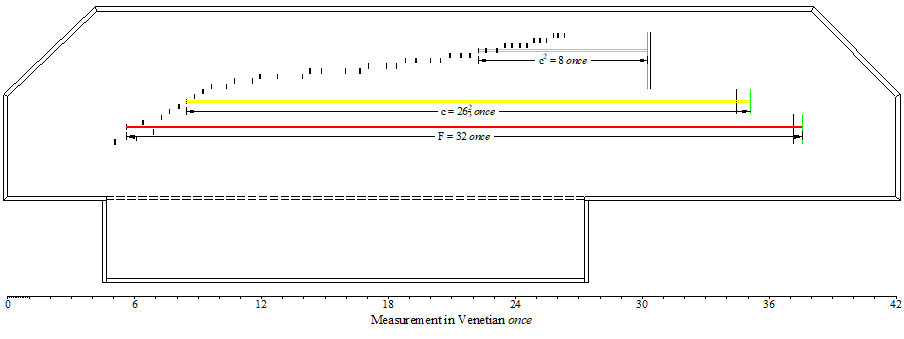
Figure 3 – Critical design scalings, the proposed bridge positions (in green), and the fret positions
Leipzig Musikinstrumentenmuseum der Universität, Clavichorde Cat. No. 1
A numeric analysis of all of the string lengths is given below in Table 6
|
Played note |
Sounded note |
Measured length |
Corrected length |
Design length |
Corrected length in once |
Design length in once |
Size of chromatic semitones |
Size of diatonic semitones |
Size of major second |
|
c3 |
g3 |
117½ |
114.8 |
116.6 |
3.96 |
4.02 |
|
|
|
|
b2 |
f#3 |
126 |
123.3 |
124.8 |
4.25 |
4.31 |
|
124 |
|
|
bb2 |
f3 |
132 |
129.3 |
130.4 |
4.46 |
4.50 |
82 |
|
206 |
|
a2 |
e3 |
141 |
138.3 |
138.2 |
4.77 |
4.77 |
|
|
|
|
g#2 |
eb3 |
150½ |
147.8 |
147.9 |
5.10 |
5.10 |
|
115 |
|
|
g2 |
d3 |
159 |
156.3 |
154.6 |
5.39 |
5.33 |
97 |
|
212 |
|
f#2 |
c#3 |
168½ |
165.8 |
167.4 |
5.72 |
5.78 |
|
|
|
|
f2 |
c3 |
178 |
175.3 |
175.0 |
6.05 |
6.04 |
96 |
|
|
|
e2 |
b2 |
188½ |
185.8 |
187.2 |
6.41 |
6.46 |
|
101 |
197 |
|
eb2 |
bb2 |
198½ |
195.8 |
195.6 |
6.76 |
6.75 |
91 |
|
191 |
|
d2 |
a2 |
210 |
207.3 |
207.4 |
7.15 |
7.16 |
|
|
|
|
c#2 |
g#2 |
224½ |
221.8 |
221.9 |
7.65 |
7.66 |
|
117 |
|
|
c2 |
g2 |
234½ |
231.8 |
231.8 |
8.00 |
8.00 |
77 |
|
193 |
|
b1 |
fT2 |
246½ |
243.8 |
241.9 |
8.41 |
8.35 |
|
|
|
|
bb1 |
f2 |
259 |
256.3 |
252.8 |
8.84 |
8.72 |
87 |
|
|
|
a1 |
e2 |
274½ |
271.8 |
270.5 |
9.38 |
9.33 |
|
102 |
188 |
|
g#1 |
eb2 |
287½ |
284.8 |
285.3 |
9.83 |
9.84 |
|
|
|
|
g1 |
d2 |
302 |
299.3 |
298.1 |
10.33 |
10.29 |
86 |
|
|
|
f#1 |
c#2 |
321 |
318.3 |
318.9 |
10.98 |
11.01 |
|
107 |
193 |
|
f1 |
c2 |
335 |
332.3 |
333.3 |
11.47 |
11.50 |
75 |
|
181 |
|
e1 |
b1 |
347½ |
344.8 |
343.4 |
11.90 |
11.85 |
|
|
|
|
eb1 |
bb1 |
361½ |
358.8 |
358.9 |
12.38 |
12.38 |
69 |
|
|
|
d1 |
a1 |
386 |
383.3 |
384.0 |
13.23 |
13.25 |
|
114 |
183 |
|
c#1 |
g#1 |
398 |
395.3 |
396.9 |
13.64 |
13.70 |
|
|
|
|
c1 |
g1 |
418 |
415.3 |
414.7 |
14.33 |
14.31 |
85 |
|
|
|
b |
f#1 |
450½ |
447.8 |
443.8 |
15.45 |
15.31 |
|
130 |
216 |
|
bb |
f1 |
466½ |
463.8 |
463.7 |
16.00 |
16.00 |
61 |
|
191 |
|
a |
e1 |
476½ |
473.8 |
475.2 |
16.35 |
16.40 |
|
|
|
|
g# |
eb1 |
510 |
507.3 |
508.5 |
17.51 |
17.55 |
|
118 |
|
|
g |
d1 |
534½ |
531.8 |
531.3 |
18.35 |
18.33 |
82 |
|
200 |
|
f# |
c#1 |
545 |
542.3 |
540.8 |
18.71 |
18.66 |
|
|
|
|
f |
c1 |
570 |
567.3 |
565.1 |
19.58 |
19.50 |
78 |
|
|
|
e |
b |
581 |
577.7 |
573.2 |
19.93 |
19.78 |
|
|
|
|
eb |
bb |
601½ |
598.8 |
598.9 |
20.66 |
20.67 |
62 |
|
|
|
d |
a |
733 |
749.8 |
748.7 |
25.87 |
25.83 |
|
|
|
|
c# |
g# |
745 |
761.8 |
760.7 |
26.29 |
26.25 |
|
|
|
|
c |
g |
756 |
772.8 |
772.8 |
26.67 |
26.67 |
|
|
|
|
B |
f# |
766 |
782.8 |
782.5 |
27.01 |
27.00 |
|
|
|
|
Bb |
f |
779 |
795.8 |
797.0 |
27.46 |
27.50 |
|
|
|
|
A |
e |
869 |
877.4 |
876.6 |
30.28 |
30.25 |
|
|
|
|
G |
d |
894 |
902.4 |
903.2 |
31.14 |
31.17 |
|
|
|
|
F |
c |
919 |
927.4 |
927.4 |
32.00 |
32.00 |
|
|
|
|
E |
B |
880 |
888.4 |
888.7 |
30.66 |
30.67 |
|
|
|
|
D |
A |
904 |
912.4 |
912.9 |
31.48 |
31.50 |
|
|
|
|
C |
G |
933 |
941.4 |
941.9 |
32.48 |
32.50 |
|
|
|
|
C |
G |
933 |
941.4 |
941.9 |
32.48 |
32.50 |
|
|
|
| Total in cents: | 1127 | 1028 | 2352 | ||||||
| Averaged measured size of interval in cents: | 80 | 114 | 196.6 | ||||||
| Size of ¼-comma meantone interval in cents: | 76.05 | 117.11 | 193.16 | ||||||
Table 6 – Theoretical string lengths and fretting with the bridges in their proposed positions
Leipzig Musikinstrumentenmuseum der Universität, Clavichorde Cat. No. 1
In Table 6 the played notes on each of the three bridges are indicated by the colours green, peach and violet in column 1. The grouping of the fretted notes of the 11 pairs of strings on the top bridge has also been indicated in columns 1, 5 and 7 where it can be seen that there is double-, triple-, and quadruple-fretting. It should be noted that, unlike most eighteenth-century fretting system, there are no fretting groups which are repeated from octave to octave. For example bI is fretted [bI2, b2, c3] in the top octave, [a1, bI1, b1] an octave lower, and [bI, b, c1, cT1] an octave lower still. At first this seems somewhat unusual and arbitrary. However, when examined in detail the system used here has one enormous advantage when it comes to tuning the instrument. If any one of the diatonic notes is chosen for tuning and its pitch is fixed relative to a tuning standard, then the rest of the instrument can be tuned by tuning octaves either up or down from this chosen note. This can be seen by beginning on any diatonic note on the top bridge and noting that, by tuning up or down an octave, this also tunes a major second higher or lower than the chosen note. If this is done repeatedly the result is to tune all of the 11 top strings without the necessity of having to temper any of the intervals involved: it is all done by the fretting design. Once the notes on the top bridge have been tuned, then the notes on the two lowest bridges can also be tuned in octaves in the usual way.
The critical design lengths in Venetian once have been indicated by dark blue shading of column 6 in Table 6. The measured length in column 3 is the uncorrected length of the strings with the bridges in their present positions. The corrected lengths in the next column are the lengths of the strings that would result from a movement of the top bridge (notes shaded in green) by 2.7mm toward the tangents, of the middle bridge by 16.8mm away from the tangents and a movement of 8.4mm away from the tangents for the bottom bridge. These can be compared with the design lengths, which are the lengths that I feel were used by Pisaurensis when building and designing this instrument. Remember that the bridges were moved to give exactly the desired lengths for the critical notes in the columns giving the corrected and design lengths in columns 6 and 7.
However fixing the lengths of the critical notes by moving the bridges naturally also affects the lengths of the other notes on the bridges. The lengths of the longest string in each of the fretted groups is indicated in the design length column with light blue shading. It is clear that, having moved the bridges by the necessary amounts to give the desired critical lengths, this then gives lengths for the lowest note of each of the fretted groups which are close to a simple number or fraction of Venetian once.
[1] A book on historical stringing practice illustrating the traditions in various centres in Italy is currently in preparation by me. In the work that I have done so far preparing this book I have been able to show how the local unit of measurement relates to the string scaling design and to the use of the most common stringing materials of iron, yellow brass and red brass.
[2] See footnote 6.
[3] Karin Richter, who has made a copy of this instrument, has pointed out to me that the two bass bridges are slightly too high in their present positions so that the strings are not all in the same plane. Moving the two bass bridges away from the tangents and down the right-hand sloping soundboard section as suggested here would have the result of bringing all of the strings closely to the same level for all three bridges.
![]()