A virginal by Franciscus Patavinus dated 1552 in the Museo Correr, Venice

          As explained above, in Venice and throughout the rest of the Italian peninsula, the baseboard dimensions without the case sides were chosen in simple units or fractions of the inch or oncia[7] (plural once) that the maker was using.  Since the oncia was normally divided into twelve equal parts each called a line or linea (plural linee) it is to be expected that fractions involving twelfths, sixths, thirds, quarters and halves of the oncia would be involved in the design and execution of the instruments[8].  The Venetian foot or piede[9] (plural piedi) had a length close to 347.76mm[10], and this was divided into 12 giving an inch or oncia of 28.98mm. 

          The Museo Correr on the Piazza San Marco in Venice holds a fine Italian virginal signed: ‘ ~  FRANCISCI  PATAVINI  DICTI  HONGARO  MDLII  ~ ’ [11].  The namebatten and the signature are definitely not original to the instrument.  The signature is written on a piece of wood foreign to the rest of the instrument, and this wood appears to be fir or spruce stained brown to match the appearance of the cypress used elsewhere in the instrument.  The fact that the nameboard and signature are not original to the instrument does not, however, mean that its maker is not Francesco Patavinus[12].  Indeed the mouldings on the instrument are not even the same as those of the two other extant instruments thought to be by Franciscus Patavinus[13].  However here, as with other makers I have studied where there is a lack of correspondence of the mouldings, I do not see any reason for doubting that any of these instruments are by Patavinus[14].  Although he seems consistently to have signed himself ‘FRANCISCVS PATAVINVS DICTI [H]ONGARO’ so that he appears both to have had Hungarian roots and to have come from Padova, he is almost certainly to be identified with the ‘Francesco dalli arpicordi’ and the ‘Francesco dai manicordi’ who appears in the Venetian archives[15] and who lived and worked there.

          Figure 1 shows a schematic representation of the case mouldings, the keywell scrolls, and the bridge section at the position of the c² string of the 1552 polygonal virginal by Franciscus Patavinus in the Museo Correr, Venice.  The application of the case sides to the outer edge of the baseboard, and the additional height of the case sides resulting from the extra depth added by the top cap moulding and ivory studs are clearly indicated here.

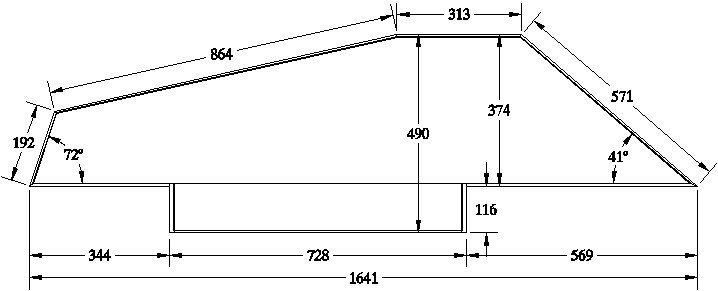
          Unfortunately the usual catalogue measurements of Italian and Venetian virginals (Table 1 and Figure 2) are taken of the outer case sides and, to my knowledge, never of the baseboard on its own.  Hence the normal catalogue measurements do not normally enable one to make any sort of an analysis of the size of the baseboard from which the maker began the design and construction of the instrument.  It is therefore necessary to measure the baseboard without the case sides and then to analyse these measurements. 

Figure 1

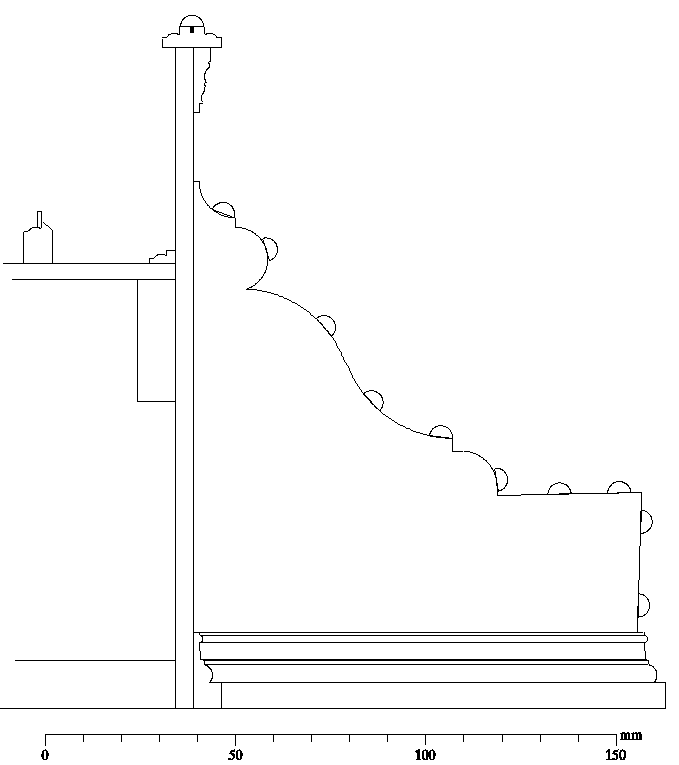
Schematic representation of the case mouldings, the keywell scrolls,

and the bridge section at the position of the c² bridge pin.

Polygonal virginal by Franciscus Patavinus, 1552

Museo Correr, San Marco, Venice

                                                           Dimension         Height*       Thickness         Wood

                                       Front:                 1641                172-4             5.4-6.4            cypress

          Case left of the keywell:                  344               173½-4               6.4               cypress

                      Angled left side:                  192                  173                  4.7               cypress

                     Angled left back:                  864                  172                  5.0               cypress

                                        Back:                  313                  173                  5.1               cypress

                    Angled right side:                 571                 172-3                 5.2               cypress

        Case right of the keywell:                 569                 172-4                 5.4               cypress

            Outside of the keywell:                 728                   ---                    ---                    ---

                              Total width:                 490                   ---                    ---                    ---

                        Keywell scrolls:            project 116            136                   11                cypress

                               Baseboard:                       Italian style                    12.4-12.8             fir**

                                     Angle at the left-front corner:       72º

                                   Angle at the right-front corner:       41º

* These heights do not include the top cap moulding which adds a further 5mm to each measurement.

** As there are no pitch pockets in this large piece of wood, it is almost certainly of fir and not of spruce.

 Table 1

Outside dimensions in mm including the case sides, but not the outer mouldings

Polygonal virginal by Franciscus Patavinus, 1552

Museo Correr, San Marco, Venice

Figure 2

Outer dimensions in mm including the case sides, but not the outer mouldings

Polygonal virginal by Franciscus Patavinus, 1552

Museo Correr, San Marco, Venice

          Table 2 and Figure 3 show the baseboard measurements in millimetres of the 1552 Franciscus polygonal virginal without the case sides.  A number of these are given in Table 2 in their nominal measurement in Venetian once.  Many of these show a close agreement between the measured length in millimetres and a simple nominal number of Venetian once, and strongly suggest that this was the unit of measurement used in the design of the baseboard of this instrument.  However the measurements of the sloping edges at the left- and right-hand sides of the case do not give measurements which can be expressed in whole numbers or simple divisions of the Venetian oncia.  This suggests that the measurements of these sloping edges are not those that were used by the maker in the design of the instrument.  The angles at the extreme ends of the virginal are also not simple numbers like 30º, 60º or 45º, or even simple angles based on multiples of 5º or 10º.  These two facts must therefore somehow be related.

          To understand this relationship and how the front corner angles were constructed it is necessary to examine their geometry.  The tangent[16] of the angle at the left-hand corner, for example, is:

tan 72° = 3.07 ≈ 3 =

This suggests that the sloping surface at the left-hand side of the instrument was made up by drawing the hypotenuse of a triangle with orthogonal sides that are in the ratio of 3 once:1 oncia, 6 once:2 once, 9 once:3 once, etc.  The actual measurement of the sloping side of just over 6 once immediately suggests that the two orthogonal sides of this triangle were designed by Patavinus to be 6 once and 2 once.  Similarly at the right-hand corner the tangent of the angle there gives

tan 41° = 0.869 =  ≈

and suggests that the angle formed at this corner resulted when Patavinus drew the hypotenuse of a right-angle triangle with sides 12½ (the width of the instrument) and 14½ once. 

          Figure 4 shows the dimension in millimetres of the baseboard in directions perpendicular and parallel to the front of the instrument, and indicates the close agreement between the measurements at the front of the case with simple units of the Venetian oncia.  Figure 5 shows the lengths of each of the sides of the baseboard of the Franciscus Patavinus virginal as it must have been designed by Franciscus, with the calculated angles at the front corners which would result from their construction using triangles with sides measured in simple numbers of Venetian once.  The agreement between the measured values of both the lengths and of the front corner angles makes clear the design of the baseboard of this instrument by Franciscus in units of the Venetian oncia. 

          Other dimensions such as the maximum case height of 174mm (6.004 once) also give simple units of the subdivision of the Venetian piede.  In fact the Franciscus Patavinus virginal shows the use of the local unit of measurement in many other aspects of its design which have not been shown here.  But the dimensions and balance point of the keyplank (ie. of the jointed board from which the keys were cut), the string scalings, the angling of the strings, the dimensions of the blocks from which the boxslide was made, etc. were all based on the use by Patavinus of the Venetian oncia.  The dimensions of the Patavinus virginal show the use of simple units of the Venetian oncia in a manner that is particularly simple and clear.  The dimensions of other instruments sometimes involve slightly more complicated numbers, and may involve subdivisions of the oncia, soldo or pollice into thirds, sixths and twelfths, as well as the more usual halves and quarters.  Some of these are illustrated in the examples discussed below.

                                                                                  Measured             Nominal dimension

                                                                                  dimension              in Venetian once

                                                                                       mm                     mm            once

                                                           Length:               1622                   1622.9           56

                                                            Width:                359*                   362.3           12½

                                Case left of the keywell:                348                     347.8            12

                                            Angled left side:                183                       ---            (6.31)

                                           Angled left back:                862                       ---           (29.74)

                                                              Back:                304                     304.3           10½

                                          Angled right side:                555                       ---           (19.15)

                              Case right of the keywell:                565                     565.1           19½

                                                       Keywell:                709                     710.0           24½

                                           Keywell projects:                116                     115.9             4

                                   Maximum case height:                174                     173.9             6

* The more-or-less unaltered length of the keywell braces indicates that the wood of the baseboard has shrunk and that this measurement was probably originally about 362mm.

Table 2

Dimensions of baseboard without the case sides and mouldings

Polygonal virginal by Franciscus Patavinus, 1552

Museo Correr, Venice

Figure 3

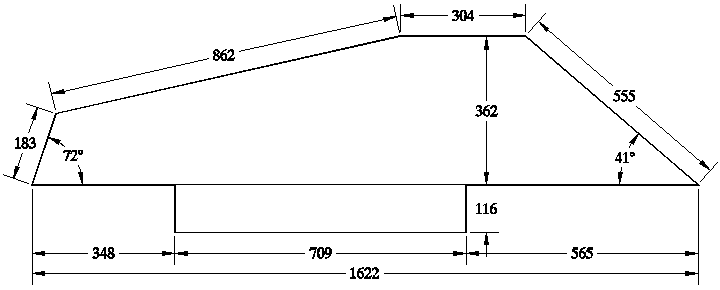
Measured dimensions in mm of the baseboard without the case sides

and measured angles at the front corners

Polygonal virginal by Franciscus Patavinus, 1552

Museo Correr, San Marco, Venice

tan 72° = 3.07 ≈ 3 =                       tan 41° = 0.869 =  ≈

Figure 4

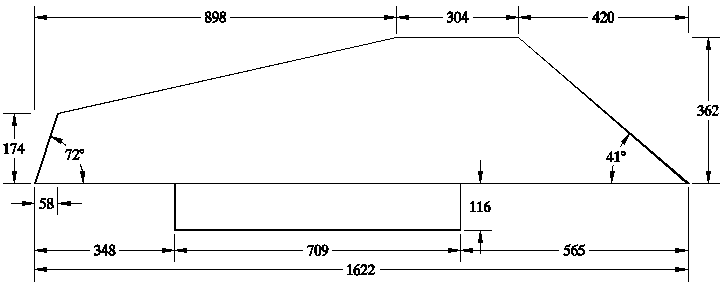
Measured dimensions in mm of the baseboard without the case sides

and measured angles at the front corners

Polygonal virginal by Franciscus Patavinus, 1552

Museo Correr, San Marco, Venice

At the front left-hand corner:                                     At the back:

            174mm = 6.004 once                                                420mm = 14.49 once

              58mm = 2.001 once                                                898mm = 30.99 once

                                                                                            304mm = 10.49 once

Figure 5

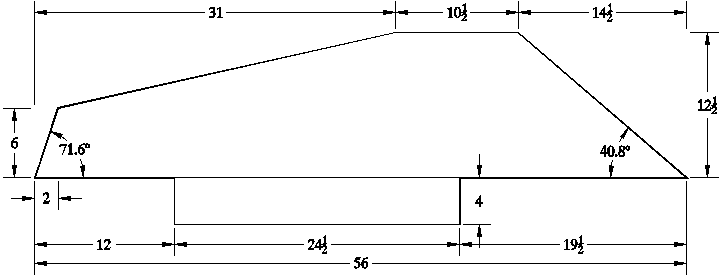
Baseboard dimensions without the case sides measured in the Venetian oncia = 28.98mm

showing the front corner angles calculated from these.

Polygonal virginal by Franciscus Patavinus, 1552

Museo Correr, San Marco, Venice

tan 71.6° = 3 =                              arctan  = 71.6°

tan 40.8º = 0.862 =              arctan  = 40.8º

          The virginal by Franciscus Patavinus was clearly designed using the Venetian oncia of length 28.98mm.  The baseboard measurements make this particularly obvious, and also show that the various angles were drawn, not by using a protractor, but by drawing the diagonal of a rectangle with sides which were a simple number of Venetian once in length.  The position and length of the long diagonal side at the rear left-hand side of the instrument was drawn by joining the end of the near left-hand sloping side and a point on the rear of the baseboard which was 31 once in from the left end.  Hence the irregular pentagonal shape of the baseboard arises from a series of orthogonal measurements, perhaps drawn out on a jointed plank that was originally 56 once (4½ Venetian piedi) long by 12½ once wide.  The close agreement between the measured angles at the front corners of the baseboard and the angles calculated theoretically from the orthogonal components of the sides used to construct them is a further confirmation of the method used by Franciscus to construct the baseboard.

          Working in reverse in those instruments where the centre in which they were built is not known it is possible to use the angles at the front corners to guess what the measurements used to construct them was, and from this to make an initial guess at the length of the unit of measurement.  This will be illustrated in the examples below.  In harpsichords the tail angle was normally constructed in a similar way, and using this angle to guess at the orthogonal components of the angle used to construct it can enable one to make an initial guess at the length of the unit of measurement used in the design and construction of all of the rest of the instrument.

Click here to go to the next section

Click here to return to to main page of the section on Italian Geometry

Endnotes: